Multi-UAV reinforcement learning with temporal and priority goals

Master of Science in Engineering in Computer Science

Unmanned aerial vehicles (UAVs) are becoming more and more in demand, their use initially spread for the execution of military missions, now it is becoming increasingly popular in the civilian field. UAVs are involved in the most exterminated missions. In this thesis, we address the problem of the risk of conflicts between UAVs and then analyze it in a specific scenario. Minimizing the risk of collision is extensively covered in the BUBBLES project. The BUBBLES project is a large project funded by the European community, coordinated by the Universitat Politècnica de València with the participation of the DIAG, Sapienza University of Rome coordinated by Prof. Luca Iocchi. The focus of the Sapienza unit is to implement methods to generate many trajectories for risk assessment.

Scenario Characteristics

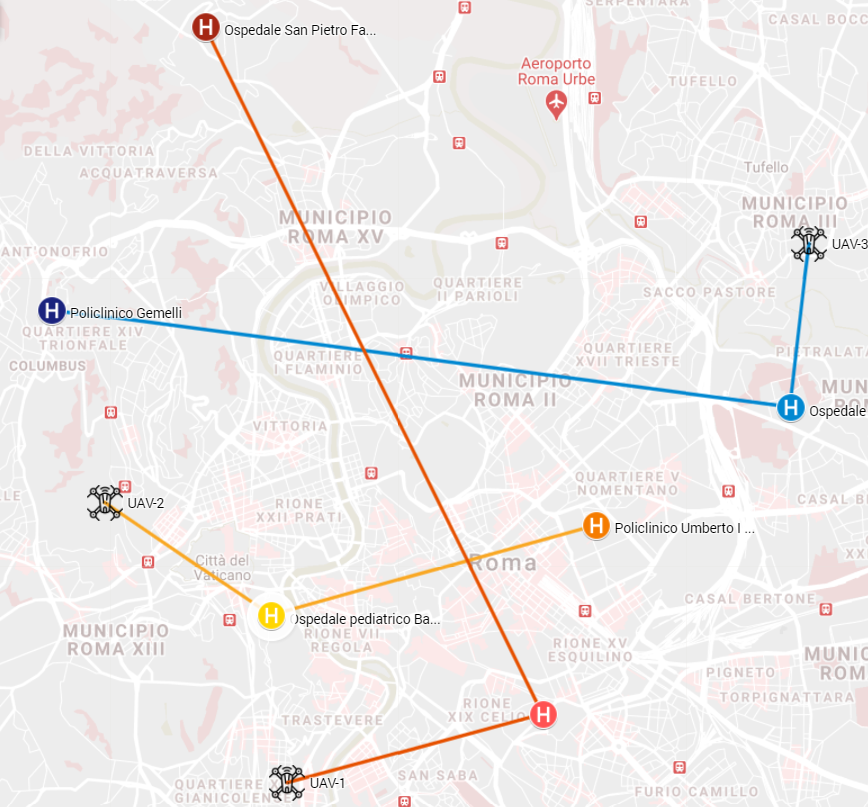
As it was previously said, the application scenarios in which UAVs can be used are very many, the scenario that is examined in this thesis project concerns the delivery of medical supplies between hospitals in a metropolis. In our scenario, hospitals in the city of Rome are represented on the grid. Each hospital can request medicines, organs, vaccines, blood from one of the other $\mathcal{n-1}$ hospitals in the city.

Scenario

Each UAV must take the resource from a specific hospital and deliver it to the hospital that requested it. UAVs must visit hospitals in a given order and must respect the mission priority assigned to them.

Another main goal is to reduce to 0 or in any case minimize the possible collisions between UAVs.

Objectives of the abstract problem

The objectives of the abstract problem are:

1. Find an optimal policy for each agent, reducing interference between agent policies
2. Agents must respect the mission priority associated with each goal and reach the goals in the correct order

Assumptions

• We assume a global clock, which measures the time during the evolution of the scenario for each agent $\alpha_i$, from 0 to T.
• Let’s consider a set of asynchronous goals, in which each agent can decide to execute its task at any time independently from the other agents.
• Each agent does not know where the other agents are at any given instant of time.

Problem Definitions

The scenario of our case study is a tuple defined as follows:

A Scenario $\mathcal{S} = \langle \mathcal{A, M, RB} \rangle $.

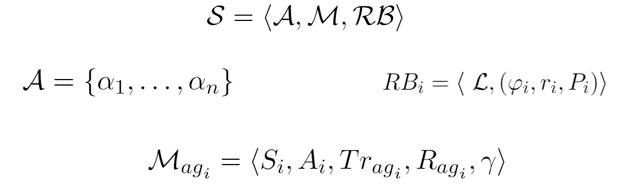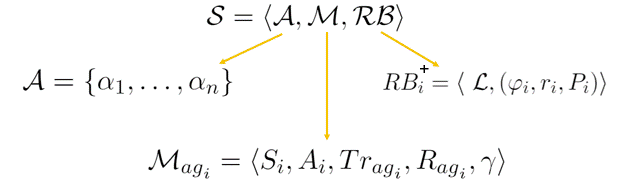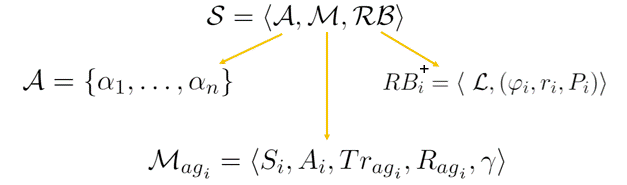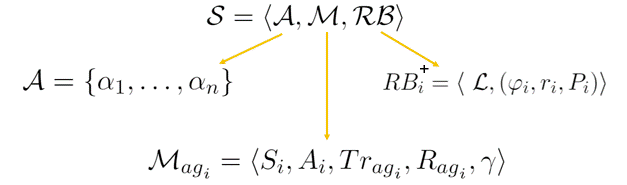Scenario definition

Where $\mathcal{A}$ is the set of agent $ \alpha_i $ modelled by the MDP, in our case each agent is a UAV. $\mathcal{RB}$ is the set of Restraining Bolts, which define the behaviour of the UAV to reach the goal. The agent interacts with the $ W $ world through actions $ A_i $.

Restraining Bolt augmented

$\mathcal{RB_i^\mathcal{+}}=\mathcal\langle\ \mathcal{L}, (\varphi_{i}, r_{i}, P_{i}) \rangle$

The behaviour of each agent is learned through the use of Reinforcement Learning and Restraining Bolt. Restraining Bolt was introduced in 2019 by (De Giacomo et al., 2019) restraining , this thesis work extends the original $\mathcal{RB}$ by adding the concept of priority.

Each $\mathcal{RB}$ is a tuple that contains:

• $\mathcal{L}$ is the set of fluids, in the case study is the colours assigned to hospitals
• each agent $\alpha_i$ has a goal ($\phi_i, P_i$) where is the LTLf/LDLf formula that the agent must satisfy.
• $P_i$ is a non-negative integer associated with this formula to indicate its priority.
• $r_i$ is the reward associated with formula $\phi_i$

Reinforcement Learning + Restraining Bolt augmented

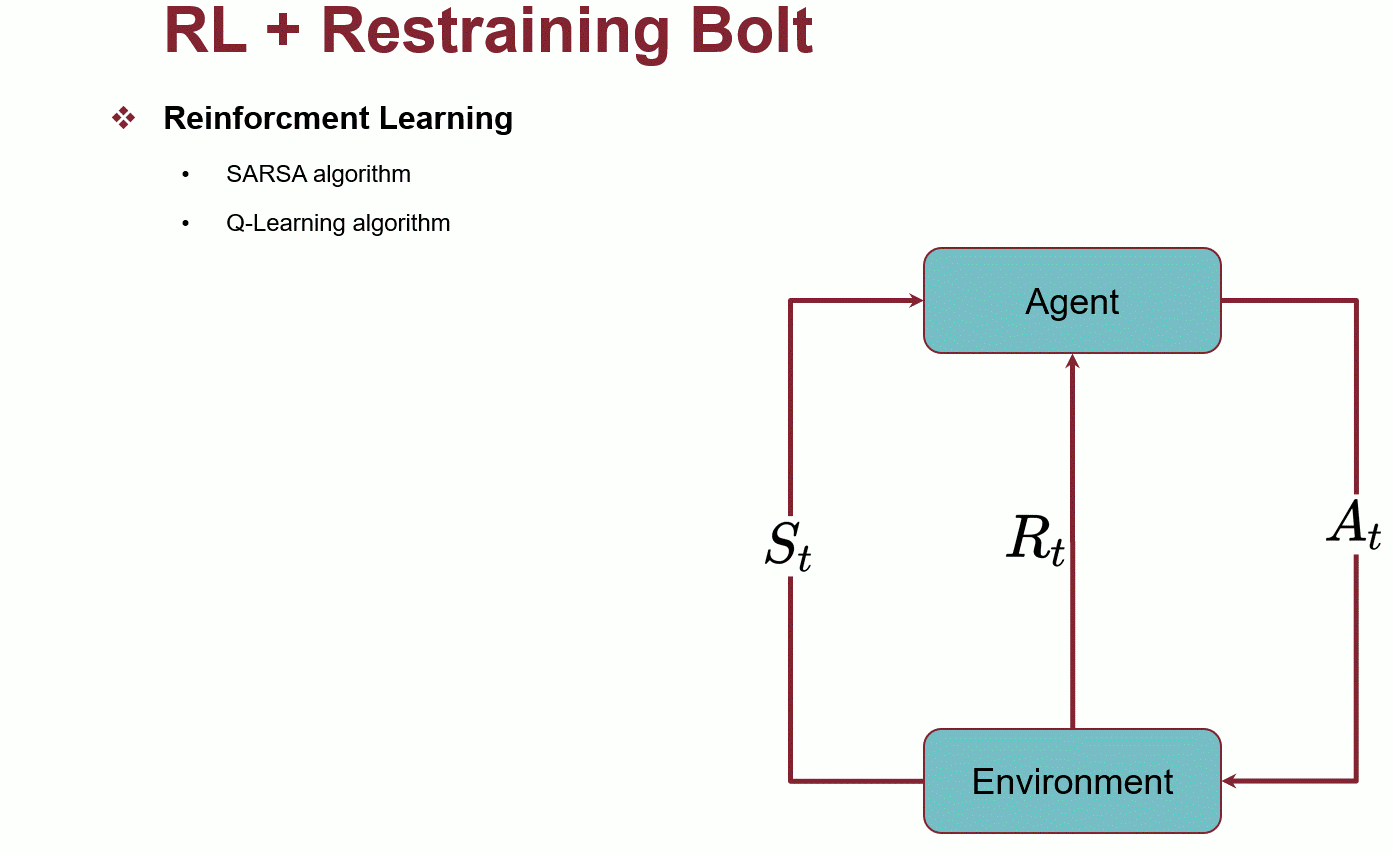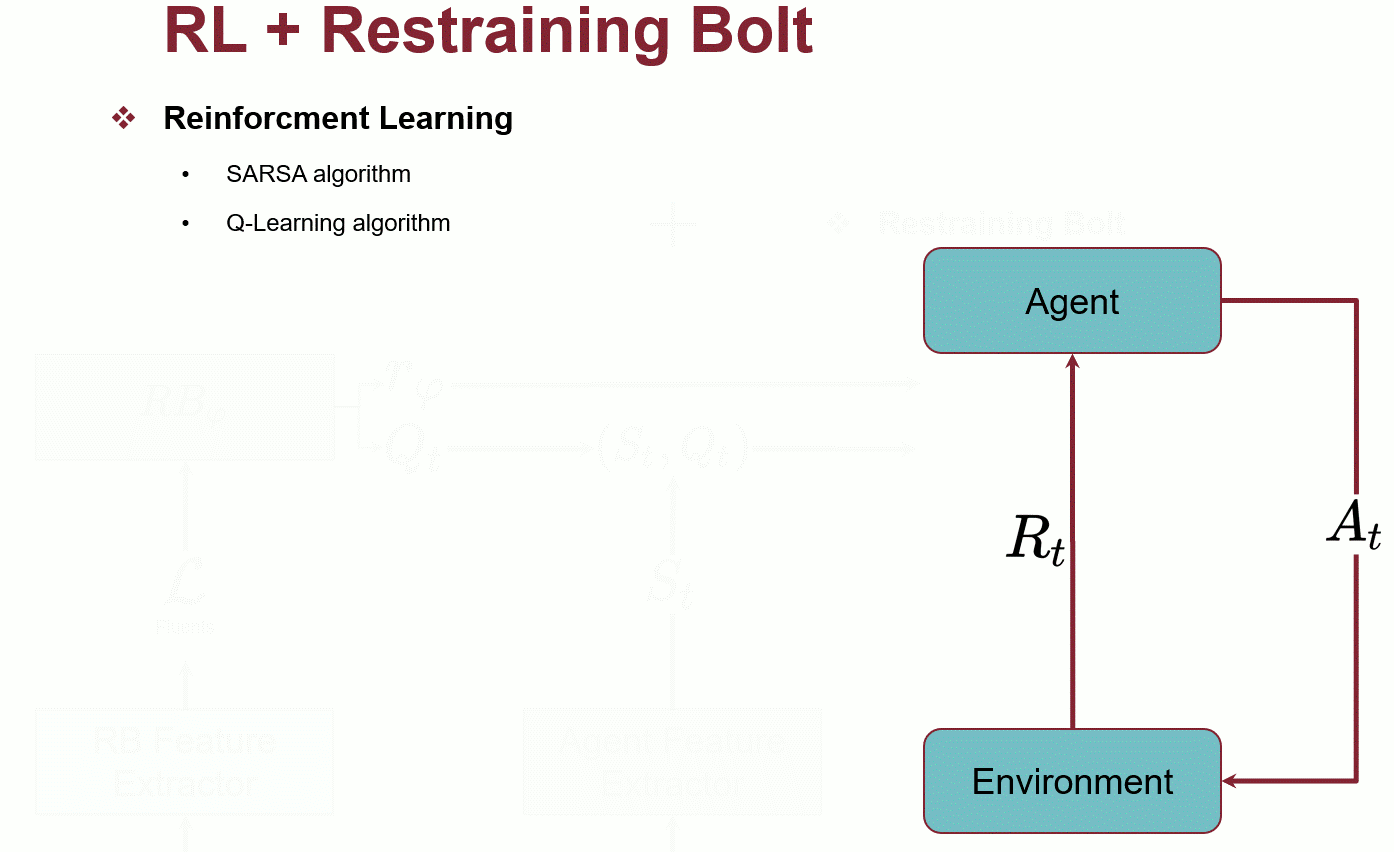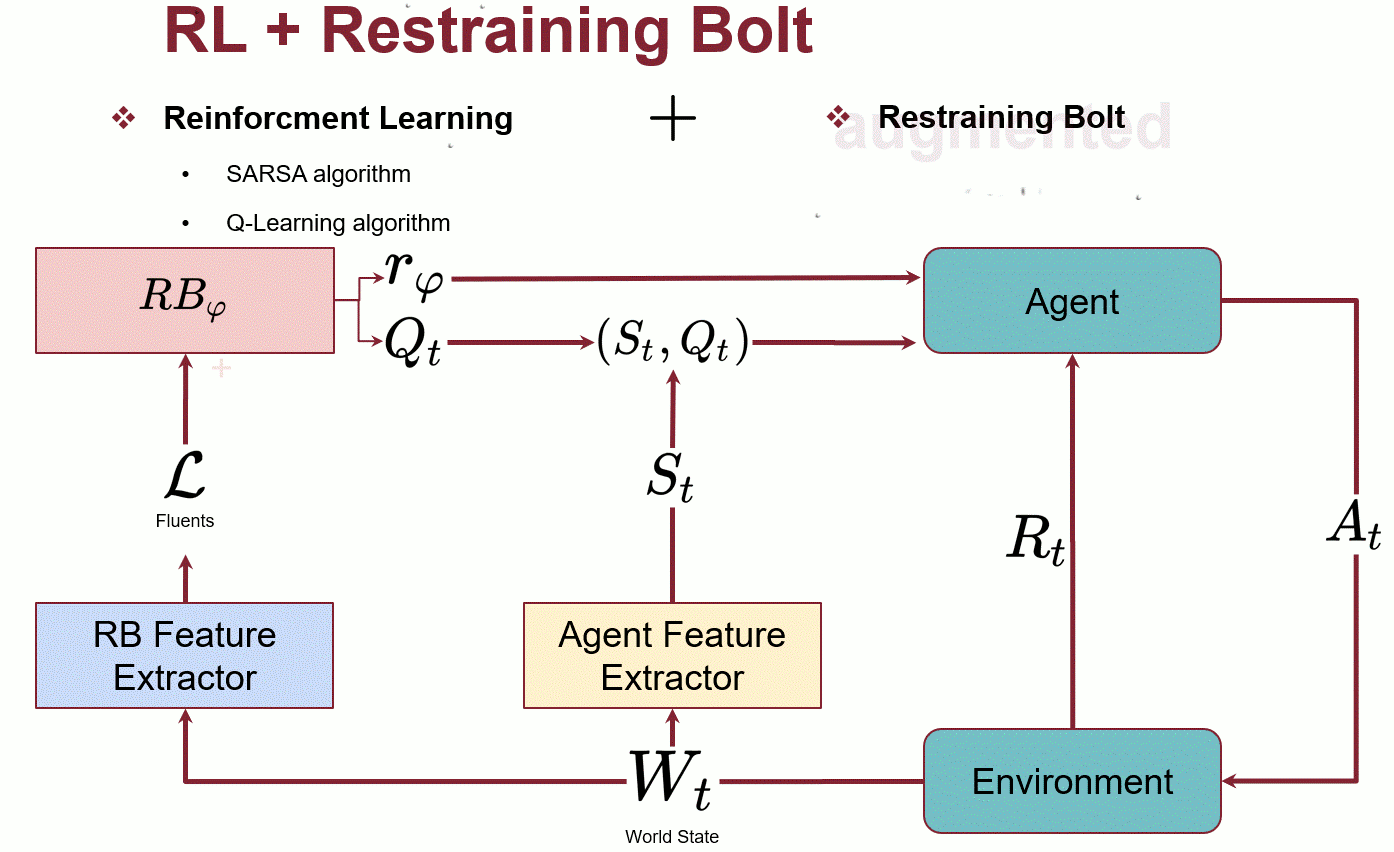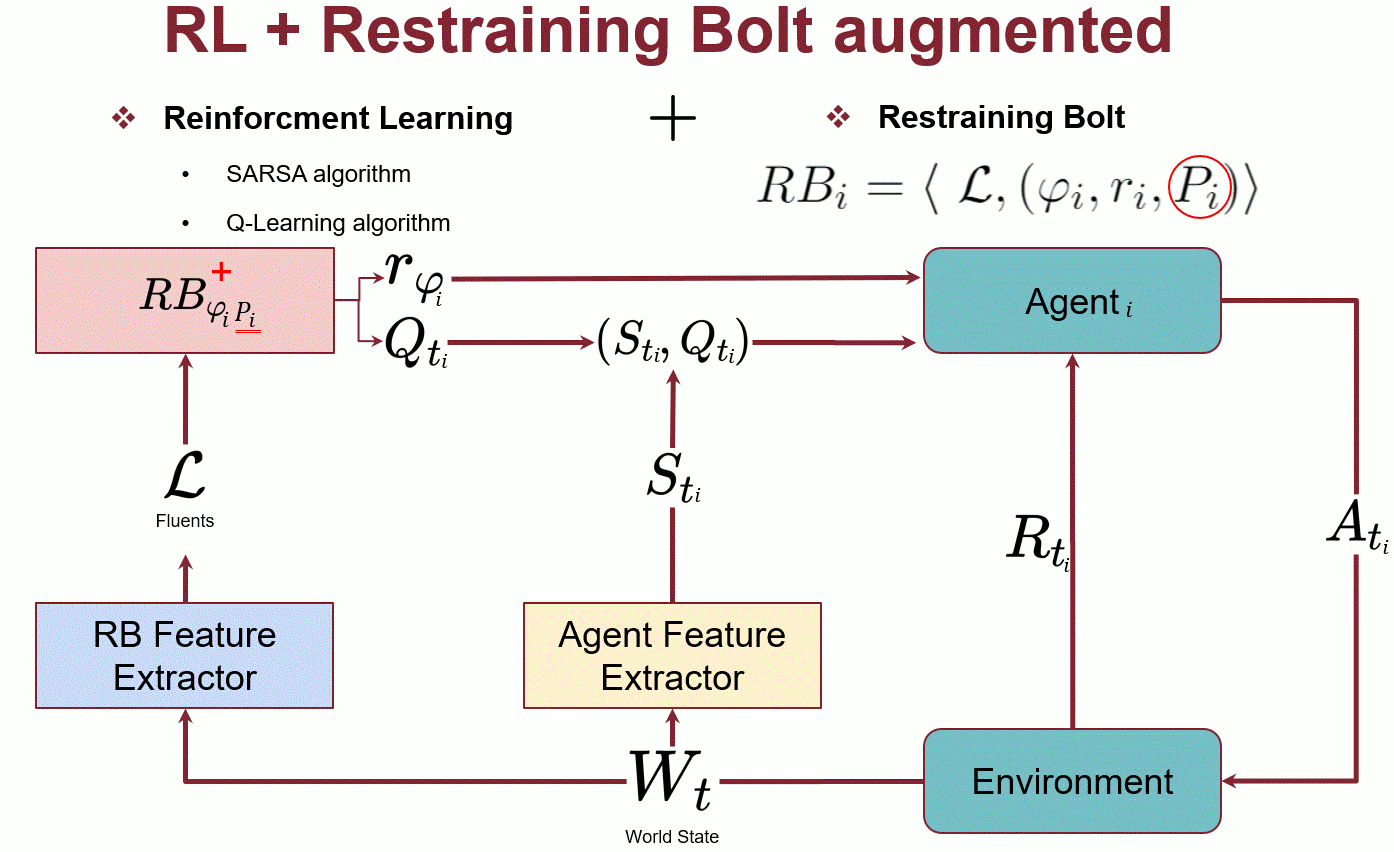
In the RL the agent performs an action and receives a reward and an observation from the environment. With the Bolt, the agent receives two independent rewards, one from the MDP for each state/action and another from the $\mathcal{RB}$ based on the state of the automata, which follows the satisfaction state of the $\phi_i$, formula.

Reinforcement Learning + Restraining Bolt augmented

Each agent will try to maximize the rewards to find an optimal policy. The concept of priority permits finding incremental policies. The system is scalable, and each agent learns independently.

Proposed Solution

Minimizing the risk of collision is a fundamental requirement to carry out Multi-UAV missions safely, this requirement is more important than efficiency and must be guaranteed. Another fundamental objective of this thesis is the management of missions according to their priority. Hence, each UAV must reach its goal in the shortest possible time based on the priority of the task assigned to it, ensuring safety.

Our solution is given to find $n$ policies $\rho_{\mathcal{a g}_{i}}$, one for each agent $\alpha_i$, that are individually optimal concerning each agent’s goal, and that in the case of conflicts, they are always resolved in favour of the agent who has a goal with higher priority (lower value of $P_i$).

To eliminate interference between agent policies, we define a new “no-interference” reward function $ N_{\mathcal{ag}_{i}}$ for each agent. The $ N_{\mathcal{ag}_{i}}$ function is computed by applying, to the original reward function $R_{\mathcal{ag}_{i}}$ a modifier $\mathcal{\tau_i}$ that depends on the trajectories generated by the execution of the optimal policy $\rho_{\mathcal{a g}_{i}}$ of agents with higher priority goals. Each agent must satisfy its $\varphi_{i}$ formula and must respect the priority value assigned to this goal.

• If the agent $ \alpha_i $ has $ P_i = 0 $ (highest priority), then $ N_{\mathcal{ag}_{i}}$ equals the reward function $ R_{\mathcal{ag}_{i}}$.
• If the agent $ \alpha_i $ has $ P_i > 0 $, then $ N_{\mathcal{ag}_{i}} $ reward function is the sum of the reward function $ R_{\mathcal{ag}_{i}}$ of the agent $\alpha_i$ and of a modifier $\mathcal{\tau_i}$ that depends on the trajectories generated by optimal policies of agents $\alpha_j$ for which $P_j < P_i$.

More formaly:

$N_{\mathcal{ag}_{i}} = R_{\mathcal{a g}_{i}} + f ( { \tau_j | \alpha_j \ s.t.\ P_j < P_i })$

$ N_{\mathcal{ag}_{i}} $ is defined on the basis of the policies obtained from the agents $\alpha_j$, who have a higher priority $P_j < P_i$.

Note that, we admit non-deterministic behaviour during optimal policy execution. However, we assume that the variability of the trajectories is limited so that it is possible to define a modifier function $f$ removing interference.

Case study

The case study is a model of our hospital’s problem in which the world is represented in a grid. $\mathcal{RB_i}$ gives a positive reward if the agent does hovering/beep in the right order on the cells of the hospitals. In our case, the no-interference reward has been implemented by adding negative weights on the cells crossed by the trajectories of the previous agents.

The missions of each UAV is specified by LDLf formulas

The LTLf/LDLf formulas specify the mission of each UAV and the temporal order of the goals. The RL algorithm used for the experiments is SARSA, State – action – reward – state – action, but we should use also other RL algorithms.

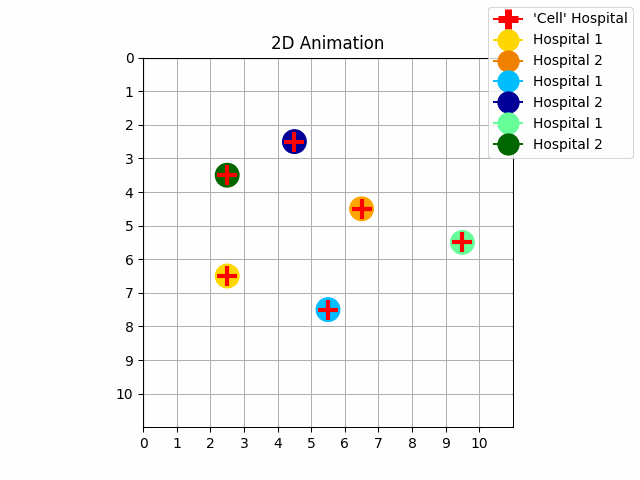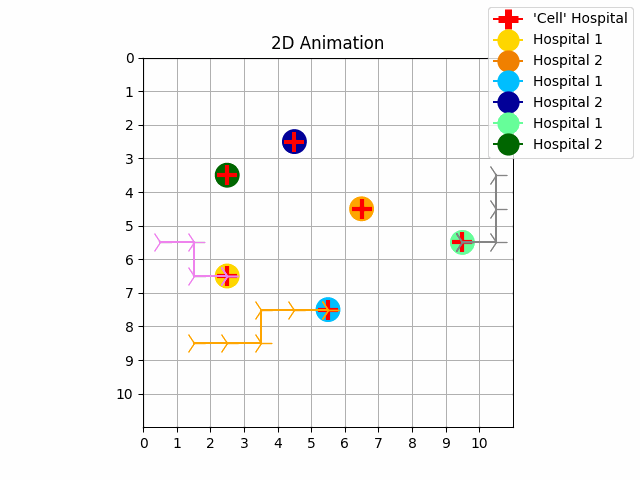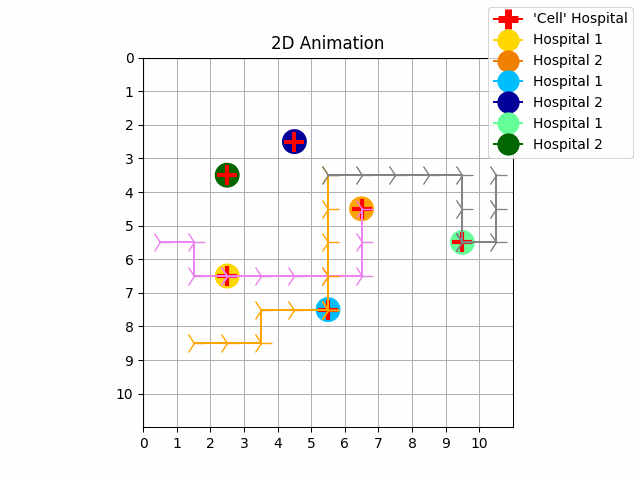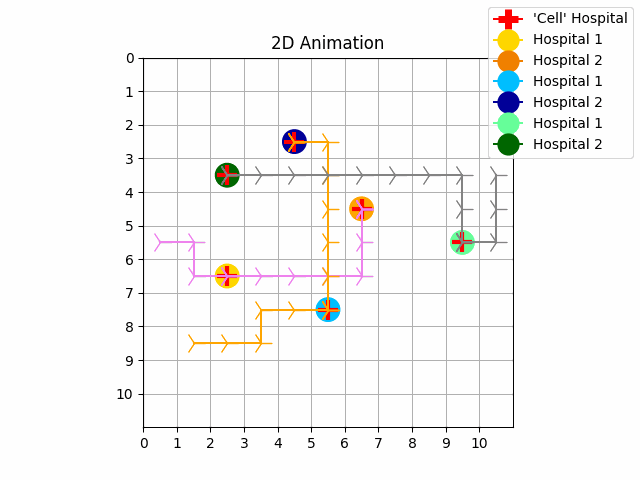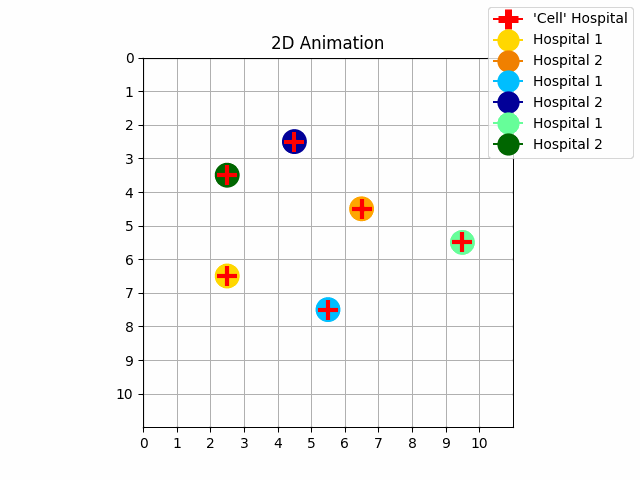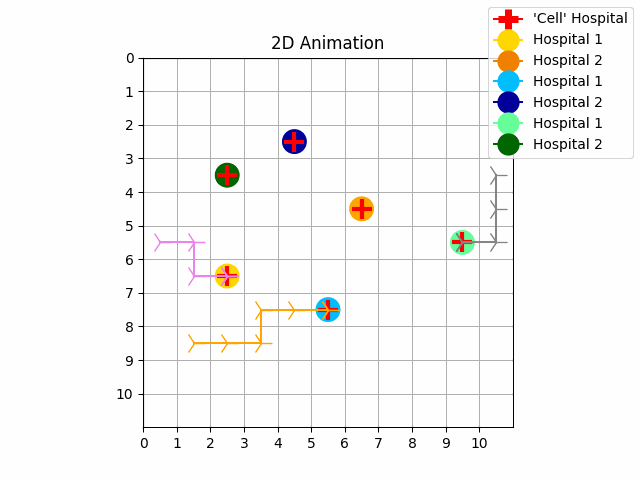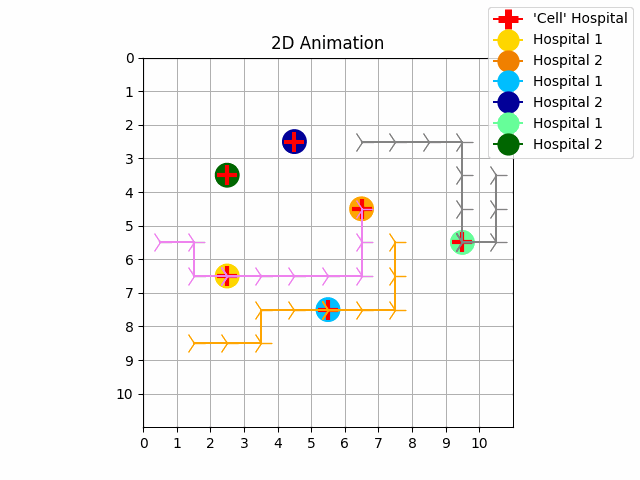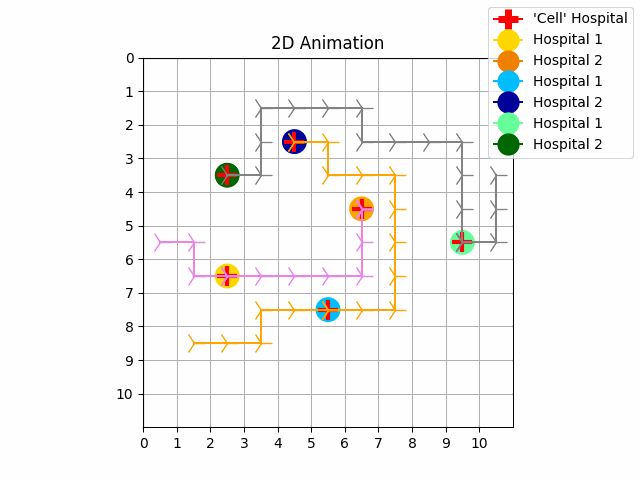Experiment 3. Without priority	Experiment 4. With priority

As we can see in experiment 1 without priority, the trajectories of the UAVs intersect with each other. In experiment 2 we resolve these conflicts with priority and with our no-interference reward functions. The purple UAV has the highest priority so its trajectory is the same in both experiments. The orange UAV has priority 1, and the grey UAV has priority 2. It is possible to perform experiments by increasing the size of the map, the number of goals and agents.

Conclusion

Our system is scalable, and we can generate hundreds of trajectories at a lower cost than a standard Multi-agent algorithm, in which case the cost would be exponential. Our method finds an optimal policy for each agent, reducing interference between agents policies. From the execution of the policies, we generate trajectories with a lower frequency of conflict.

MSc. Thesis - Alessandro Trapasso

MultiUAV-RL-RB

---